Month: April 2023

The Power of AI through the lens of Gödel’s work

Kurt Gödel, born on April 28, 1906, was an Austrian mathematician, logician, and philosopher. He made significant contributions to the fields of logic, mathematics, and computer science, leaving a lasting impact on our understanding of the foundations of mathematics and the nature of computation.

Gödel’s most significant achievements are his incompleteness theorems, which revolutionized the field of logic and mathematics.

  1. First Incompleteness Theorem: In any consistent, formal axiomatic system that is strong enough to include arithmetic, there exist statements that can be neither proven nor disproven within the system. In other words, there will always be undecidable statements or propositions within such systems.
  2. Second Incompleteness Theorem: No consistent formal axiomatic system can prove its own consistency. This implies that if a system is consistent, it cannot be used to prove that it is free from contradictions or inconsistencies.

These theorems shook the foundations of mathematics, revealing the inherent limitations of formal systems, as they implied that there would always be undecidable statements and limitations within any axiomatic system. This was a death knell to David Hilbert’s formalist program, which aimed to provide a complete, consistent, and decidable foundation for all of mathematics.

The Church-Turing thesis, posits that any function that can be computed by an algorithm can be computed by a Turing machine, effectively defining the boundaries of computability. It provides a formal framework for understanding the limitations of algorithmic computation, just as Gödel’s incompleteness theorems did for formal axiomatic systems (like arithmetic). Turing’s development of the Universal Turing Machine, a theoretical device capable of simulating any other Turing machine, provided a way to demonstrate the undecidability of the halting problem, which asserts that it is impossible to determine, whether a given program will halt or run indefinitely. This result mirrors the inherent limitations revealed by Gödel’s incompleteness theorems, as both highlight the existence of uncomputable and undecidable problems within their respective domains.

As we embarked on the exploration of computability, completeness, and consistency within a structured framework, we discovered that the prevailing themes emerging from this inquiry are “uncomputable,” “undecidable,” and “incomplete”. In recent times, a new phenomenon has come into existence, Artificial Intelligence (AI), which appears to be taking over the world. AI, often asking audacious questions and seemingly possessing infinite knowledge, gives the impression of knowing everything and wielding immeasurable power. This remarkable technology has transformed various aspects of our lives, from automating mundane tasks to making complex decisions but it is not a panacea for all human challenges. It is crucial to recognize that, just like the systems studied in mathematical logic, AI is also bound by certain inherent limitations. The very principles of Gödel’s incompleteness theorems, which unveiled the boundaries of formal axiomatic systems, serve as a reminder that AI, despite its impressive capabilities, is not all-powerful.

This begs the question, “What does power mean”?

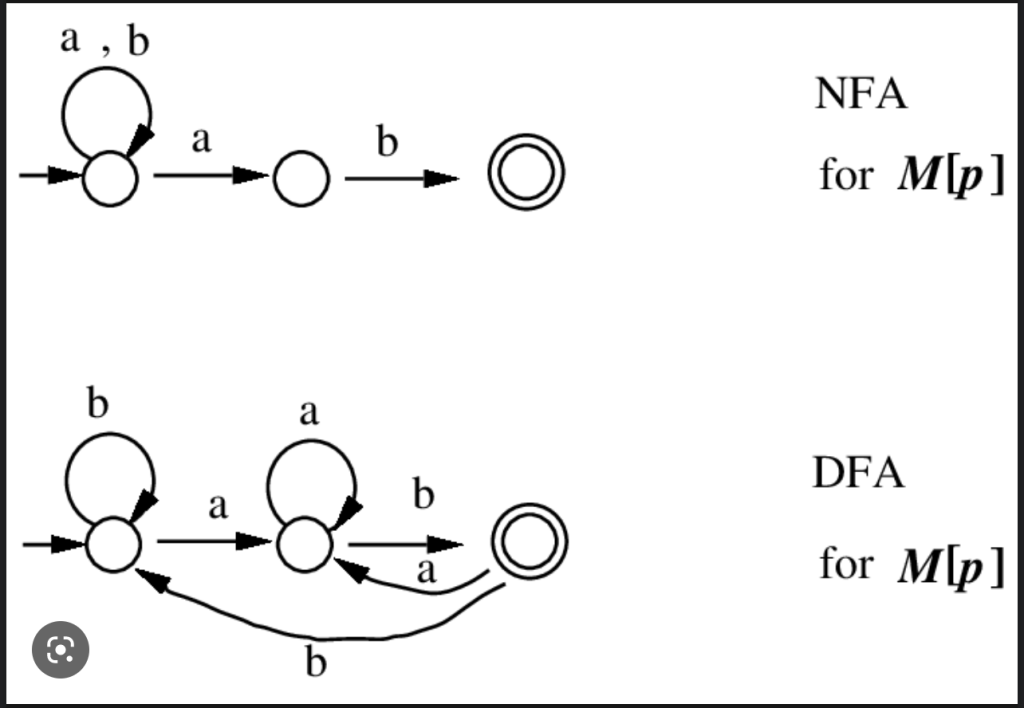
To illustrate this, I will reiterate that DFA and NFA are of equal power. It is important to note that an equivalence exists between formal logic (propositional, 1st order, 2nd order etc…), languages/grammars (regular, CFG, CSG etc..), and the theory of automata/machines (DFA/NFA, PDA, Turing machine etc…). This equivalence signifies that statements made within one domain can be translated to another while retaining their original meaning and impact.

NFAs allow multiple transitions for each input symbol and can exist in multiple states simultaneously, DFAs have a single, uniquely determined transition for each input symbol. Despite the increased flexibility of NFAs, they possess the same computational power as DFAs, illustrating that having more options (or doing more in one time unit) does not always result in greater capabilities. This observation is similar to the advantage that a lever or a pulley offers in the realm of mechanics. These simple machines provide positional advantage, allowing a person to perform the same amount of work but more efficiently or with less effort.

This observation aligns with Gödel’s incompleteness theorems, which revealed the inherent limitations of formal axiomatic systems. It suggests that no matter how advanced AI becomes, it will always be subject to constraints arising from the fundamental nature of mathematics and logic (because those are the fundamental building blocks on which the AI is built). Just as the computational power of NFAs and DFAs is equivalent despite their differences, AI’s vast access to information and computational prowess does not guarantee its ability to conquer every problem or answer every question. Instead, AI remains subject to the same limitations as any formal system, reminding us that even the most powerful tools have boundaries and that human ingenuity and agency must continue to play a critical role.

To elucidate the concept further, “power” in the context of formal systems pertains to “expressiveness.”

  1. The more expressive a grammar is, the greater the power of the language it generates. For instance, the language of palindromes possesses less power than the language {a^n b^n c^n | n ≥ 1}. The latter exhibits a higher degree of expressiveness, as it can generate a broader range of patterns beyond palindromes, thereby demonstrating its superior capabilities in terms of language generation and complexity.
  2. The more powerful a logical system is, the better it can reason. If we take the first order and second order logic, while both systems use predicate symbols and quantifiers, they differ in their expressiveness and the types of objects they can quantify over. The former allows us to express relationships between objects, properties, and quantifiers while the later allows to do over relations and functions, which are more higher level objects

In the realm of Artificial Intelligence, “power” may be interpreted as “Inclusiveness.” A highly powerful AI system is characterized by its ability to embrace, consider, and act in a manner that fosters the well-being of all individuals, surpassing the limitations of conventional computational tools and models. As each person is on their own unique journey, AI aids by addressing survival tasks and empowering them to delve into introspective questions such as “What constitutes my well-being?”, “Where am I headed?”, and “Who am I?” By fostering this level of introspection and self-awareness, AI can truly claim to be more powerful!

As we celebrate Gödel’s birthday, we honor his enduring legacy, which continues to inspire researchers and thinkers across disciplines. His work remains a testament to the beauty and complexity of mathematical inquiry, challenging us to grapple with the limits of human understanding and to push the envelop in our quest for knowledge.

Entanglement, Double Slit, Observer, Mind, Freewill

I have been meaning to connect these dots for a while and this weekend took up to task to pen down the first draft

Nobel Prize in Physics 2022 on Entanglement

The Nobel Prize in Physics 2022 was awarded jointly to Alain Aspect, John F. Clauser and Anton Zeilinger “for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science.” Quantum entanglement is a phenomenon in which pairs or groups of particles are generated or interact in ways such that the quantum state of each particle of the pair or group cannot be described independently – instead, a quantum state may be given for the system as a whole.

The violation of Bell inequalities is a test of the principle of local realism, which states that objects have definite properties even when they are not being observed. The experiments of Aspect, Clauser and Zeilinger showed that objects can be entangled, and that their properties are not determined until they are observed.

Double Split Experiment

The double-slit experiment is a fundamental experiment in quantum mechanics that demonstrates the wave-particle duality of matter and the probabilistic nature of quantum measurements. The experiment involves shining a beam of particles, such as electrons or photons, through two parallel slits onto a screen. The resulting pattern on the screen is an interference pattern, indicating that the particles behave as waves and interfere with each other. However, when the experiment is observed to determine which slit the particles pass through, the interference pattern disappears. “Copenhagen” interpretation indicates that the act of measurement collapses the wave function and forces the particles to behave like particles instead of waves, while the “Many Worlds” interpretation suggests that the act of observation creates a branching of the universe into multiple parallel worlds, each corresponding to a different possible outcome of the experiment. In this view, the wave-like behavior of the particles is not lost when they are observed, but rather continues in the other parallel worlds.

The Tenth Man story

The story goes like this, ten boys were studying with a guru and went on a journey together. Along the way, they realized that they were one man short. Each boy counted the others and found only nine. They searched high and low but could not find the tenth man. They were all very sad and returned to the guru to report that one of them was missing. The guru asked them to count again, but this time he told them to count themselves as well. When they did this, they found the missing tenth man – himself. The guru explained to them that the tenth man was never really missing, but was always there – it was just a matter of recognizing his own self

Mind

There exists a philosophy (yoga) that defines the architecture of mind as manas, chitta, buddhi, and ahamkara.

  • Manas is the sensory or perceptual aspect of the mind. It is responsible for receiving sensory input from the environment and processing it into recognizable forms. Manas is often compared to a camera or a mirror that reflects the external world
  • Chitta is the aspect of the mind that stores impressions or memories. It is responsible for retaining past experiences and creating a sense of continuity and identity over time. Chitta is often compared to a library or a computer hard drive that stores information
  • Buddhi is the aspect of the mind that represents the higher intellect or discernment. It is responsible for making decisions based on logic, reason, and intuition. Buddhi is often compared to a judge or a guide that helps us navigate the world and make wise choices
  • Ahamkara is the aspect of the mind that creates a sense of individuality or ego. It is responsible for creating a sense of “I” or “me” that separates us from others and the rest of the world. Ahamkara is often compared to a mask or a cloak that hides our true nature. This is the trickiest of the components that acts a veil on ones true nature while at the same time “I” also induces a sense of doer ship.

The study of quantum mechanics has led us to question our classical ideas of reality and has introduced concepts such as entanglement and quantum non-locality. The double-slit experiment has demonstrated that properties do not exist until they are measured and that the act of measurement itself can affect the outcome. The 10th man story reminds us that it is not just what we measure or observe, but also how we interpret it that matters. Ultimately, this interpreter has a mind, the one that induces doer-ship, and gives the illusion of choice and freewill.

Introspect the interpreter/observer to unlock the secrets and understand it nature. Based on the experimental data above, it appears that everything is connected to everything and that its only the interpreter/observer somehow comes into existence and makes it local and limited. But this is for each one of us to realize for ourselves.